What is shear modulus?
Shear modulus defines a material’s resistance to shape change under shear forces - where parallel planes slide past one another. If a cube is subjected to a force parallel to its top face and an equal and opposite force parallel to its bottom face; its side view will deform to a trapezoid.
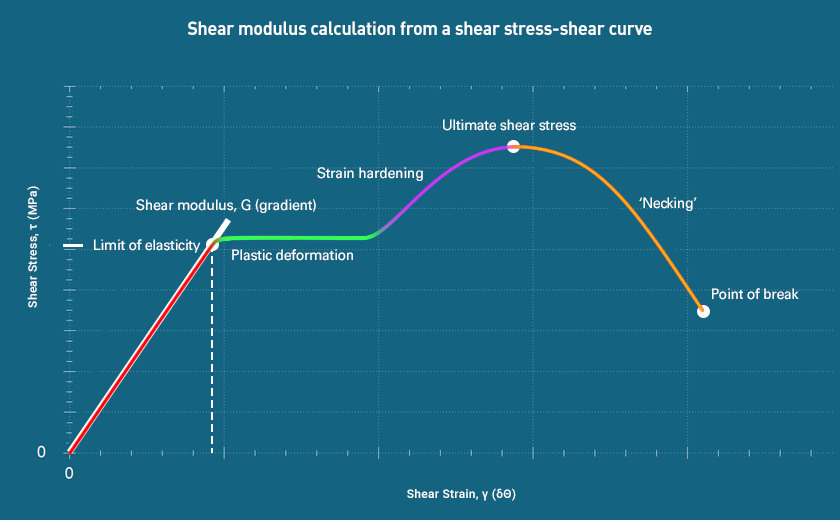
Shear modulus is one of the primary elastic moduli, alongside Young’s modulus and bulk modulus. Represented by G, it is calculated as the ratio of shear stress to shear strain within the elastic region. This property is critical in applications involving torsion, bending, or lateral loading - such as in shafts, adhesives, and elastomers.
Shear modulus formula
Where:
- G is the shear modulus (Pa or N/m²)
- τ is the applied shear stress (force per unit area, N/m²)
- γ is the shear strain (angular deformation, in radians)
This formula expresses how much a material deforms (strain) in response to an applied shear force (stress), remaining valid as long as the material behaves elastically - i.e., returns to its original shape when the force is removed.
Shear modulus equation
Shear modulus (G) and Young’s modulus (E) are both measures of a material’s stiffness - but under different types of loading. Young’s modulus describes how a material stretches or compresses under axial load, while shear modulus describes how it deforms when subjected to shear or torsional force.
For isotropic, linear-elastic materials, they are mathematically related by the following formula:
Where:
- G = shear modulus
- E = Young’s modulus
- ν = Poisson’s ratio (ratio of lateral to axial strain)
This relationship means that if any two of these properties are known, the third can be calculated. It also highlights how Poisson’s ratio affects the distribution of strain within a material and its overall rigidity in shear vs. tension.
A high shear modulus indicates greater stiffness; metals and ceramics perform well in shear - as do composites in conjunction with their lightness - while flexible materials like rubber have much lower values. The modulus of rigidity is usually quoted in GPa for more manageable numbers.
Comparison of typical G values for common material types
| Material | G (Gpa) | Type |
|---|---|---|
| Diamond | 478 | Ceramic |
| Alumina | 150 | Ceramic |
| Tungsten | 161 | Metal |
| Aluminium Nitrade | 130 | Ceramic |
| Carbon Steel | 77 | Metal |
| Iron, Ductile | 64.5 | Metal |
| Copper | 45 | Metal |
| Aluminium | 28 | Metal |
| Glass-ceramic | 26.2 | Ceramic |
| Concrete | 21 | Composite |
| Kevlar | 19 | Composite |
| Wood, Douglas Fir | 13 | Composite |
| Polyethylene | 0.12 | Polymer |
| Rubber | 0.0003 | Polymer |
FAQs about shear modulus
How is shear modulus tested?
Shear modulus is measured through torsion testing or shear testing fixtures applied to solid or bonded samples. In a torsion test, torque is applied to one end of specimen (usually round or tubular) while the other end remains fixed. The resulting angular deformation is used to calculate shear strain.
Shear testing in tension, or compression, is commonly used to evaluate adhesives, foams, and layered composites. It applies tensile, or compression, force in parallel plans to induce angular deformation in material specimens or sliding between bonded surfaces. methods such as V-notched beam and lap shear tests provide controlled loading conditions to accurately assess shear strength and stiffness in flat or bonded materials.
In which applications is shear modulus an important property?
Shear modulus determination is vital in diverse industries where material performance or movement in joints must be controlled:
- Mechanical and civil engineering - assessing torsional stiffness in shafts and beams, and the strength of bolts and fasteners in structural joints.
- Adhesive and sealant testing - where shear failure is a primary failure mode.
- Elastomer development - quantifying stiffness for gaskets, seals, and damping components.
- Composite materials - predicting interlaminar shear behaviour in aerospace and automotive sectors - lightness of engineered materials is essential - and natural composites like wood/timber.
- Geotechnical engineering - analysing the stability of soil and rock foundations in supporting civil engineering structures.
What are common test standards for shear modulus calculation?
Several international test standards define procedures for measuring shear modulus, depending on the material type, industry application and geometry:
- ASTM D5379, ASTM D7078 - V-notched beam methods for composites
- ASTM D1002, ASTM D3163 - Single-lap-shear tests for bonded metal and rigid plastics
- ASTM D5656 - Thick adherend lap shear for adhesives
- ASTM D3528, ASTM D3164 - Standards for adhesives and bonds using double and sandwich lap-shear specimens
- ASTM C273 - Shear modulus of sandwich core materials
- ASTM F606 and ISO 898 - Shear tests on bolts and fasteners
- ASTM E143 - Shear modulus by torsion for structural metals
- ISO 15310 - Torsion test method for plastics
- ASTM D143, DIN 52367 / ISO 6238 / EN 392 / BS 373 and ISO 898 - Shear strength of wood and of adhesive-bonded wood joints.
Can Mecmesin test systems measure shear modulus?
Mecmesin test systems can accept a range of interchangeable fixtures to grip material test samples or pre-prepared specimens (for example, bonded into lap or sandwiched joints, or connected via a fastener). Non-contact or optical extensometry is available for material strain deformation measurement. VectorPro test software can apply mathematical equations on supplied geometry dimensions and recorded test data to calculate modulus values.
Standards
Featured or equivalent test standards for Mecmesin solutions in this section


